In the last post, we saw that creating ten random portfolios through a Monte Carlo simulation worked pretty well. But, ten random trials isn’t very much. So, let’s see what 1,000 random portfolios look like:
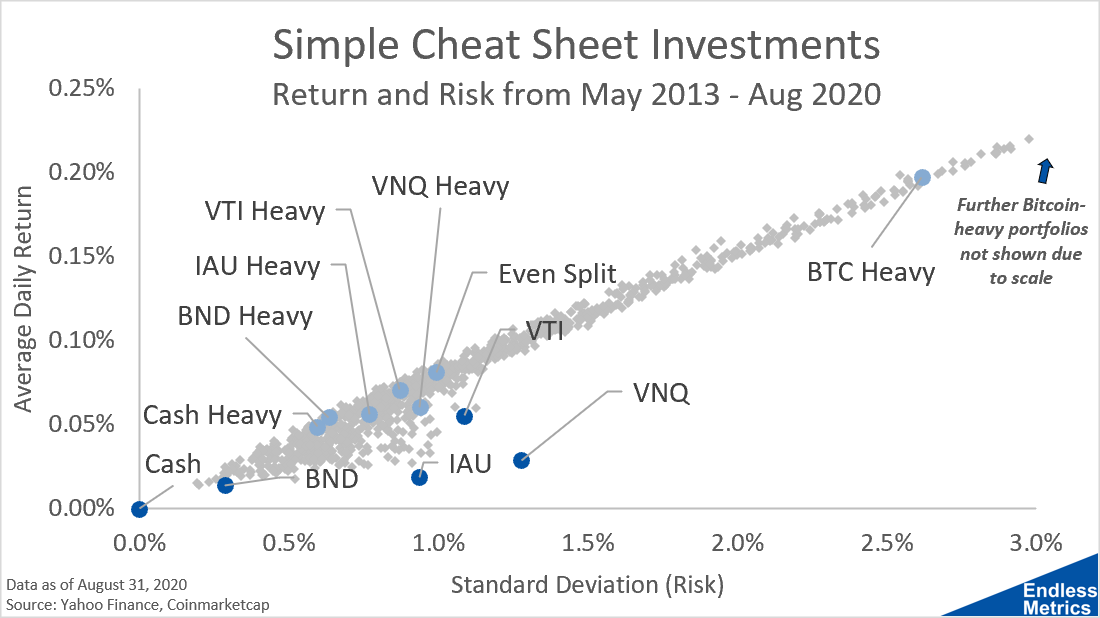
With the exception of a few portfolios, most of these trials look really good. We can start to see something resembling an efficient frontier of optimal portfolios.
One reason an efficient frontier is clearly visible after just a thousand trials is that the “random” sampling method I used is bias towards relatively equal weighting. A truly random sample would give equal selection probability to any of the possible 96 million portfolios. That is actually a bit harder to design than the simple randomization method I used for this but, to be honest, I’m fine with my simple bias method since the bias leans toward well-diversified portfolios.
With an estimate of the efficient frontier, we can now optimally tailor portfolios based on return and risk preferences. And, we achieved this with way less work than by brute force calculating the 96 million possible portfolios, approximately 0.001% of the work.
While the Monte Carlo approach is a huge upgrade over brute force, it does have the drawback of potentially not finding the absolute best portfolios possible. There is a trade off between computational effort and accuracy.
It turns out though, there is yet another methodology we can use that works even better. We will take a look at that in the next post!
